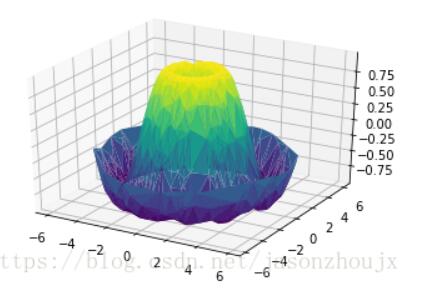
最基本的三维图是由(x, y, z)三维坐标点构成的线图与散点图，可以用ax.plot3D和ax.scatter3D函数来创建，默认情况下，散点会自动改变透明度，以在平面上呈现出立体感

三维的线图和散点图

#绘制三角螺旋线
from mpl_toolkits import mplot3d
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

ax = plt.axes(projection='3d')

#三维线的数据
zline = np.linspace(0, 15, 1000)
xline = np.sin(zline)
yline = np.cos(zline)
ax.plot3D(xline, yline, zline, 'gray')

# 三维散点的数据
zdata = 15 * np.random.random(100)
xdata = np.sin(zdata) + 0.1 * np.random.randn(100)
ydata = np.cos(zdata) + 0.1 * np.random.randn(100)
ax.scatter3D(xdata, ydata, zdata, c=zdata, cmap='Greens')

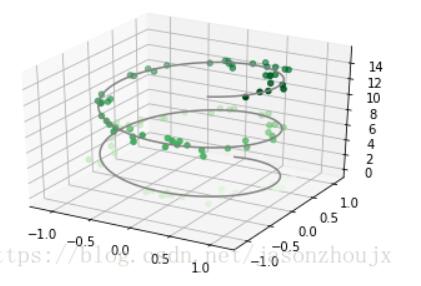
三维等高线图

def f(x, y):
    return np.sin(np.sqrt(x ** 2 + y ** 2))
x = np.linspace(-6,6,30)
y = np.linspace(-6,6,30)
X, Y = np.meshgrid(x, y)
Z = f(X,Y)

fig = plt.figure()
ax = plt.axes(projection='3d')
ax.contour3D(X, Y, Z, 50, cmap='binary')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
#调整观察角度和方位角。这里将俯仰角设为60度，把方位角调整为35度
ax.view_init(60, 35)

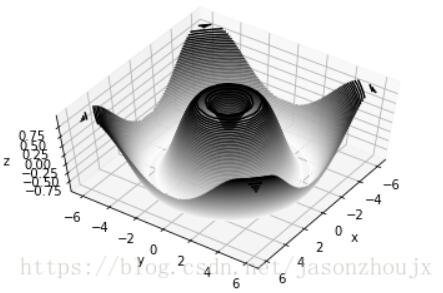
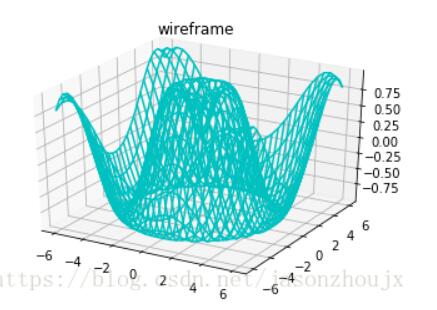
线框图和全面图

全面图和线框图相似，只不过线框图的每一个面都是由多边形构成。只要增加一个配色方案来填充这些多边形，就可以感受到可视化图形表面的拓扑结构了。

#线框图
fig =plt.figure()
ax = plt.axes(projection='3d')
ax.plot_wireframe(X, Y, Z, color='c')
ax.set_title('wireframe')

#曲面图
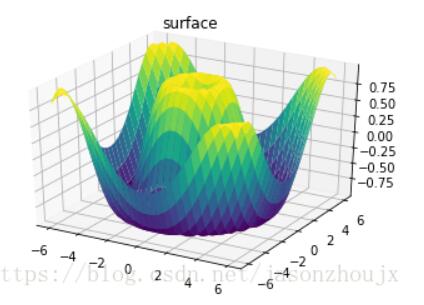
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')
ax.set_title('surface')

#使用极坐标可以获得切片的效果
r = np.linspace(0, 6, 20)
theta = np.linspace(-0.9 * np.pi, 0.8 * np.pi, 40)
r, theta = np.meshgrid(r, theta)
X = r * np.sin(theta)
Y = r * np.cos(theta)
Z = f(X, Y)
ax = plt.axes(projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis', edgecolor='none')

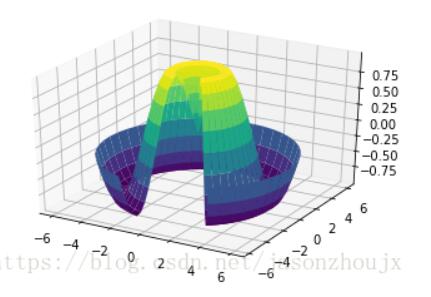
曲面三角剖分

在某些应用场景下，上述这些要求均匀采样的网格数据显得太过严格且不太容易实现。这时就可以使用三角剖分部分图形。

theta = 2 * np.pi * np.random.random(1000)
r = 6 * np.random.random(1000)
x = np.ravel(r * np.sin(theta))
y = np.ravel(r * np.cos(theta))
z = f(x, y)

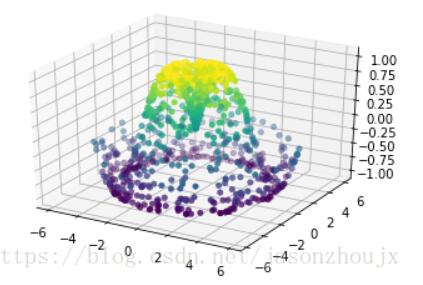
ax = plt.axes(projection='3d')
ax.scatter(x, y, z, c=z, cmap='viridis', linewidth=0.5)

#上图还有许多地方需要修补，这些工作可以由ax.plot_trisurf函数帮助我们完成。它首先找到一组所有点都连接起来的三角形，然后用这些三角形创建曲面
ax = plt.axes(projection='3d')
ax.plot_trisurf(x, y, z, cmap='viridis', edgecolor='none')