激活函数
背景
深度学习的每一个组件都需要我们理解其原理,只有掌握了基础知识,我们才能不断的优化模型和进行算法创新。本篇文章总结了 26 种激活函数,有些是非常经典的以至于原始论文无从参考,如果愿意深入研究的话可以自行搜索相关论文,至于有参考文献的,我这里都附上该函数的出处。原文链接:[Visualising Activation Functions in Neural Networks](https://dashee87.github.io/data science/deep learning/visualising-activation-functions-in-neural-networks/) ,本文在原文的基础之上做了翻译和总结,并加上详细解释,以方便日后自己使用。
激活函数简介
为什么神经网络需要激活函数
当我们不用激活函数时,权重和偏差只会进行 线性变换。线性方程很简单,但解决复杂问题的能力有限。没有激活函数的神经网络实质上只是一个 线性回归模型。激活函数对输入进行非线性变换,使其能够学习和执行更复杂的任务。我们希望我们的神经网络能够处理 复杂任务,如语言翻译和图像分类等。线性变换永远无法执行这样的任务。
激活函数使反向传播成为可能,因为激活函数的误差梯度可以用来调整权重和偏差。如果没有可微的非线性函数,这就不可能实现。总之,激活函数的作用是能够给神经网络加入一些非线性因素,使得神经网络可以更好地解决较为复杂的问题。
知乎有个提问,有不错的回答便于理解,详情可以移步:神经网络激励函数的作用是什么?有没有形象的解释? - 颜沁睿的回答 - 知乎。
改善激活函数的原因?
神经网络发展缓慢的一个因素就是激活函数最原始的时候采用了 sigmoid 函数,在传播过程中极易出现梯度爆炸和梯度消失的问题,这一点也是网络层数受到限制的原因。后来的 ReLU 可以说优化了这一点,但并没有完全解决,这篇文章介绍了当前的 26 种激活函数,方便日后选用。
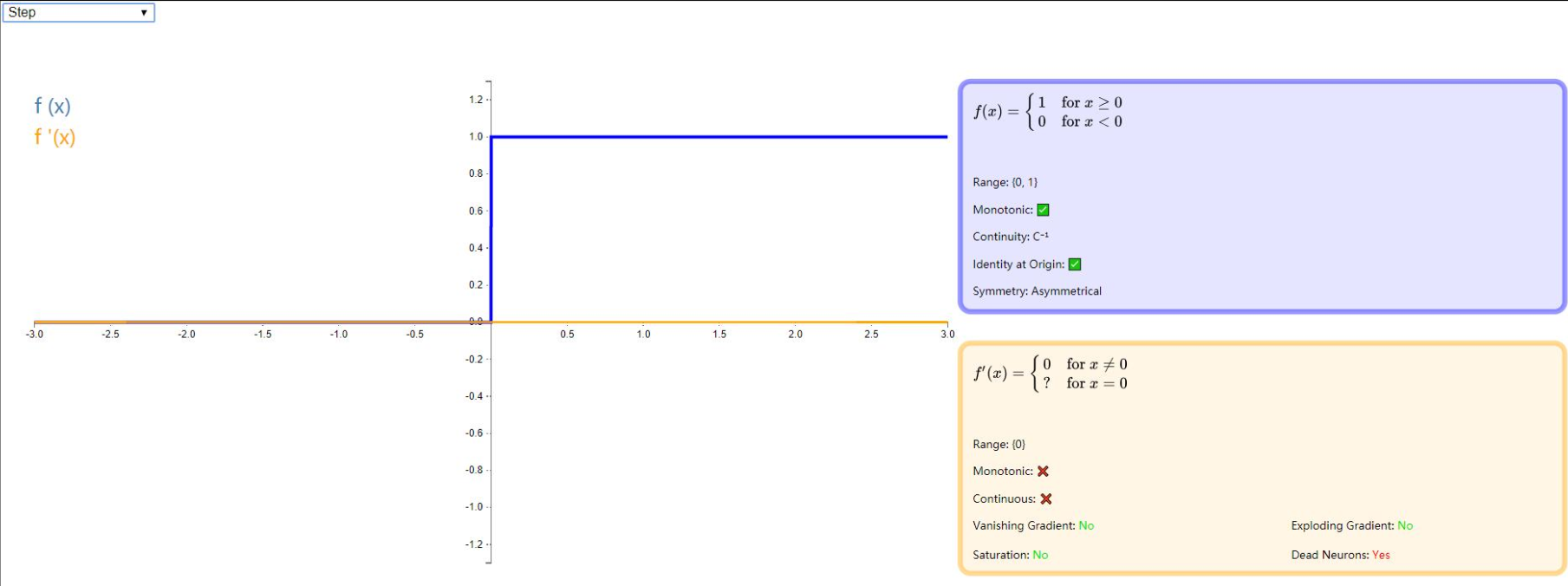
step
step 有时也被称作 Binary Step 或者 Heaviside,它的理论价值远超过其应用价值,step 能完美诠释神经元的激活含义:当刺激超过阈值的时候才会激发。但是由于它的梯度始终为 0,所以并不能用作神经网络的激活函数。详细信息请看下图:
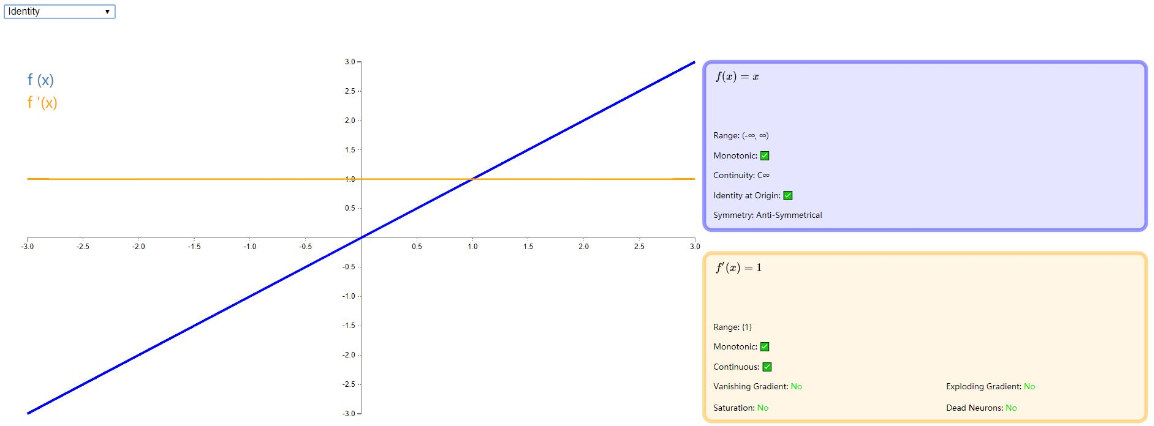
Identity
Identity 是一种输入和输出相等的激活函数,比较适合底层函数是线性的,比如线性回归问题,当存在非线性问题是,作用就大打折扣了,详细信息如下:
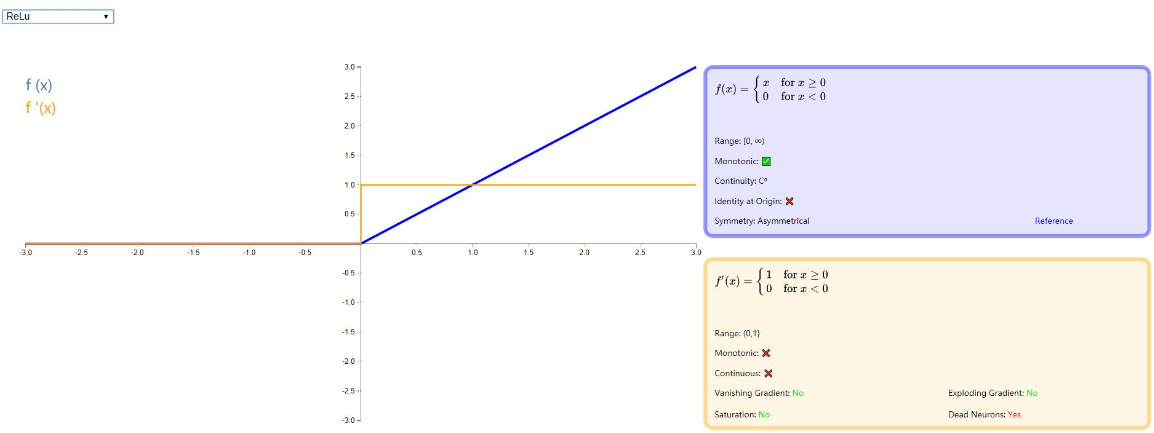
ReLU
ReLU 全称是:Rectified linear unit, 是目前比较流行的激活函数,它保留了类似 step 那样的生物学神经元机制:输入超过阈值才会激发。虽然在 0 点不能求导,但是并不影响其在以梯度为主的反向传播中发挥有效作用。有关 ReLU 的详细介绍,请移步论文:《Rectified Linear Units Improve Restricted Boltzmann Machines》 还有一篇介绍比较全的博客:神经网络回顾 - Relu 激活函数
Sigmoid
sigmoid 是使用范围最广的一类激活函数,具有指数函数形状,它在物理意义上最为接近生物神经元。此外,(0, 1) 的输出还可以被表示作概率,或用于输入的归一化,代表性的如 Sigmoid 交叉熵损失函数。
然而,sigmoid 也有其自身的缺陷,最明显的就是饱和性。从下图可以看到,其两侧导数逐渐趋近于 0 。具有这种性质的称为软饱和激活函数。具体的,饱和又可分为左饱和与右饱和。与软饱和对应的是硬饱和。
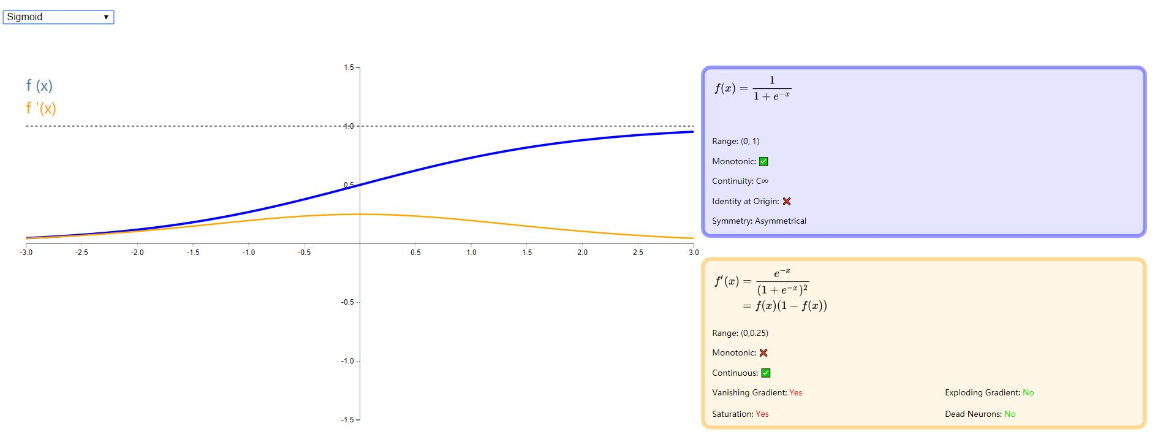
sigmoid 的软饱和性,使得深度神经网络在二三十年里一直难以有效的训练,是阻碍神经网络发展的重要原因。具体来说,由于在后向传递过程中,sigmoid 向下传导的梯度包含了一个 f′(x) 因子(sigmoid 关于输入的导数),因此一旦输入落入饱和区,f′(x) 就会变得接近于 0,导致了向底层传递的梯度也变得非常小。此时,网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说, sigmoid 网络在 5 层之内就会产生梯度消失现象。
推荐一篇介绍 sigmoid 比较详细的博客:Sigmoid 函数总结
Tanh
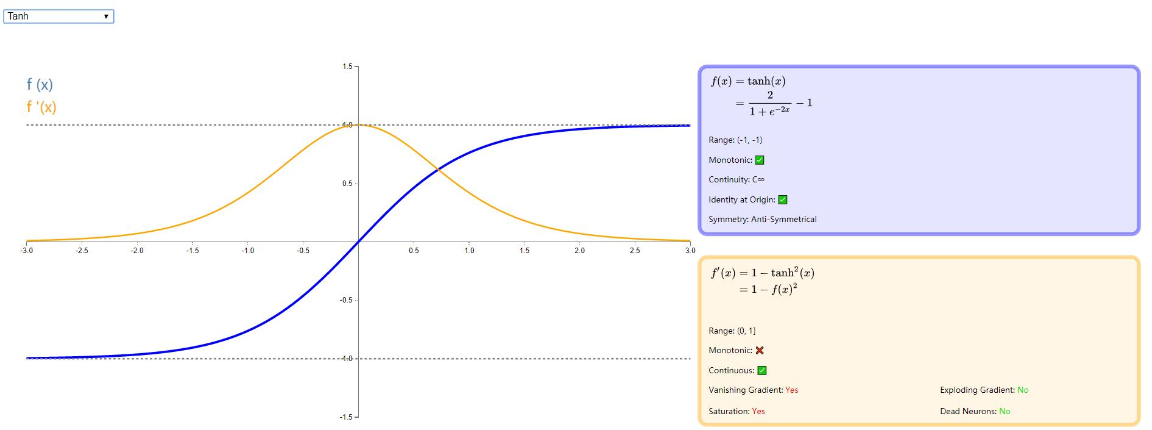
tanh 是双曲正切函数,tanh 函数和 sigmod 函数的曲线是比较相近的,咱们来比较一下看看。首先相同的是,这两个函数在输入很大或是很小的时候,输出都几乎平滑,梯度很小,不利于权重更新;不同的是输出区间,tanh 的输出区间是在 (-1,1) 之间,而且整个函数是以 0 为中心的,这个特点比 sigmod 的好。
一般二分类问题中,隐藏层用 tanh 函数,输出层用 sigmod 函数。不过这些也都不是一成不变的,具体使用什么激活函数,还是要根据具体的问题来具体分析,还是要靠调试的。
详情看下图:
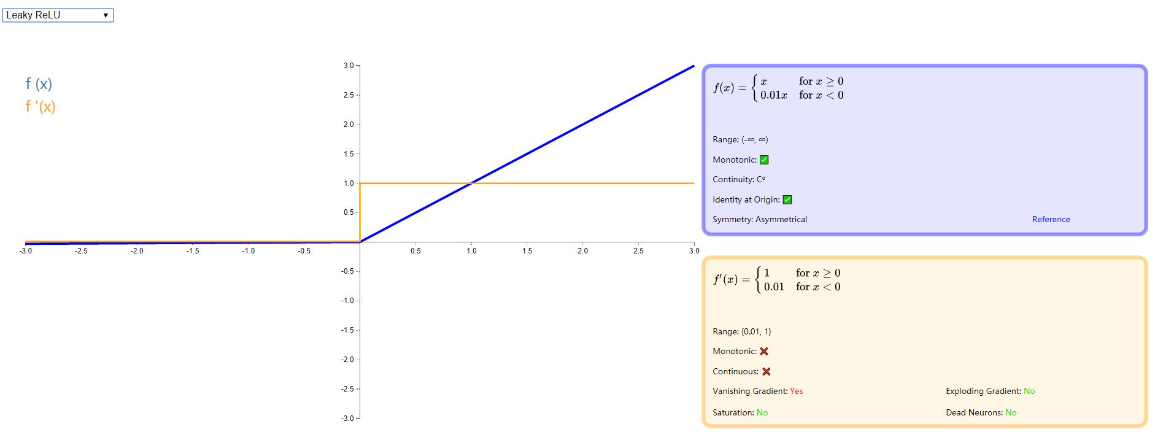
Leaky ReLU
由于 ReLU 在小于零的部分全部归为 0 ,这样极易造成 神经元死亡 ,因此 Andrew L. Maas 等人在论文 《Rectifier Nonlinearities Improve Neural Network Acoustic Models》 中提出了新的激活函数,在小于 0 的方向增加一个非常小的斜率。如下图:
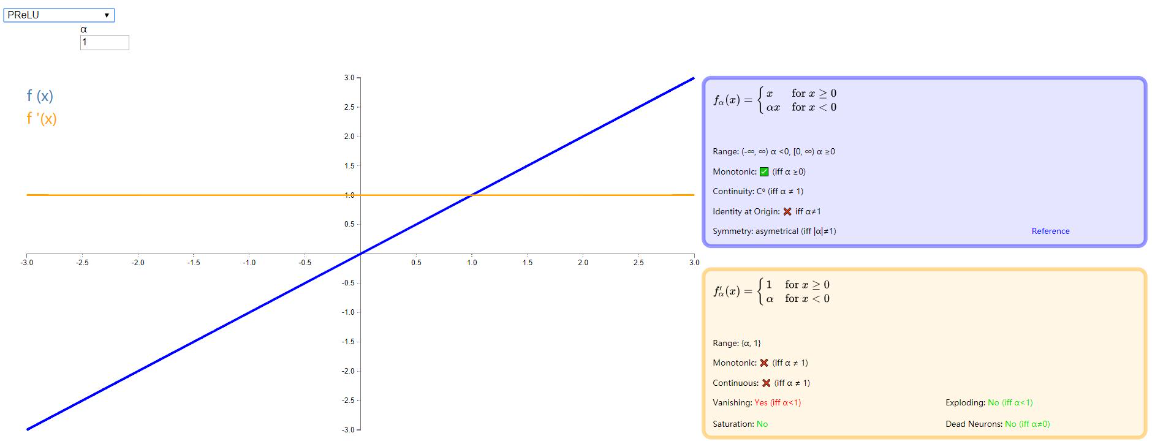
PReLU (Parameteric Rectified Linear Unit)
这个激活函数还是在优化 ReLU ,相比于 Leak ReLU,PReLU 将小于零的斜率换成了可变的参数α , 当 α<0 时取值范围为 (−∞,∞),当 α>=0 时取值范围为 [0,∞)。
详情可以参考原论文:《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》
如下图:
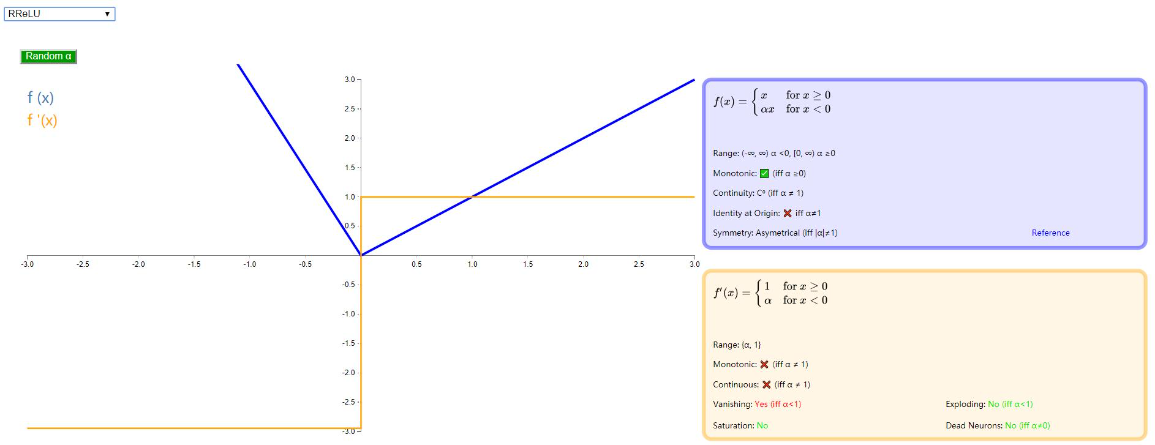
RReLU (Randomized Leaky Rectified Linear Unit)
没有太大变化,只是将 α 变成了随机数,详情可以移步论文:《Empirical Evaluation of Rectified Activations in Convolutional Network》
如下图:
ELU
前面的几种激活函数大都是对 ReLU 增加负方向的梯度,但是 ELU (Exponential Linear Units),在小于零的部分采用了负指数形式,这样的效果是使得小于零的部分具有软包和性能,一方面可以保证对输入变化的鲁棒性;另一方面其收敛速度也加快了,训练变得容易。有关 ELU 的解释可以参考论文《Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)》 和一篇博客 ELU 激活函数的提出 。图示如下:
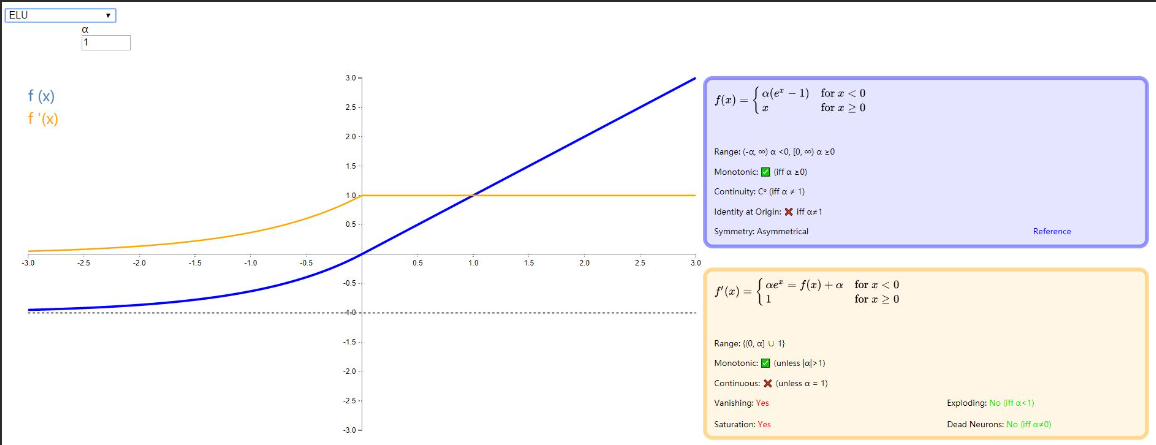
SELU
我最开始知道 SELU 的时候是在 李宏毅 的深度学习课程里,当时被它的性能给惊呆了,一度想仔细推理一下各个超参数的计算过程,但是在看了原论文 100 多页的证明过程还是先放一段时间把。附上 李宏毅 的深度学习视频:深度学习,以及 SELU 的论文:《Self-Normalizing Neural Networks》。
示例图:
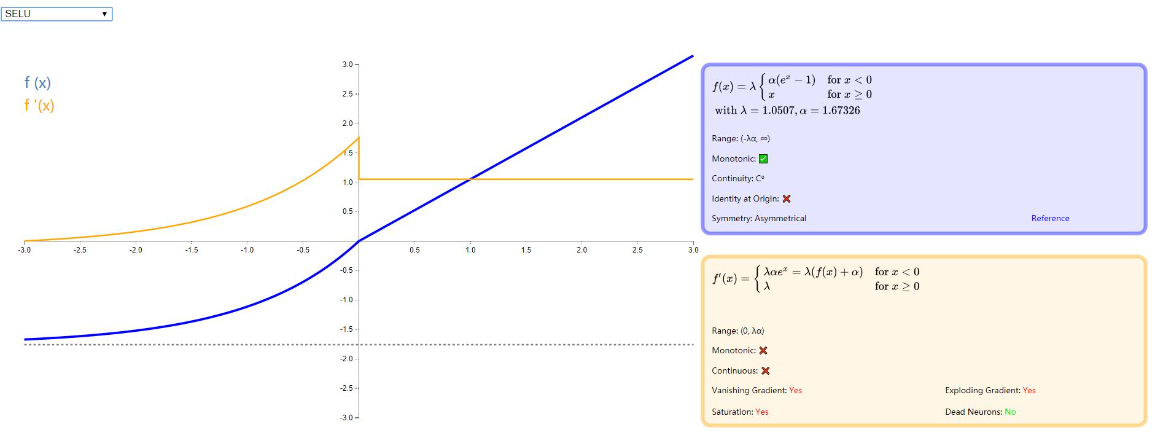
其中 λ 为固定值 1.0507009873554804934193349852946,α 也是固定值为:1.6732632423543772848170429916717,具体的推导过程在论文附录中,有兴趣的可以去看看
SReLU
SReLU 全称是 S-shaped Rectified Linear Activation Unit,也是 ReLU 系列的衍生体,由三段线性函数组合而成,具体效果怎么样没有研究过,想进一步了解的可以读一下原论文:《Deep Learning with S-shaped Rectified Linear Activation Units》。
图示如下:
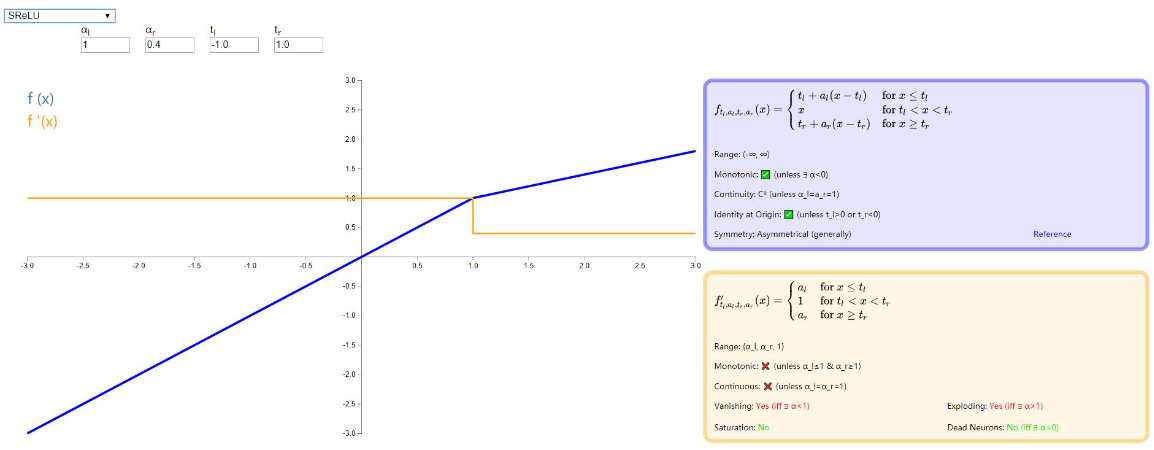
Hard Sigmoid
Hard Sigmoid 可以看做是一种以线性分段函数近似模拟 Logistic Sigmoid 的新型分类器,主要贡献体现在:计算容易和训练速度快。但是由于其在 x <−2.5 时梯度依然像 ReLU 一样为零,所以在训练过程中也会出现神经元死亡的现象。
更详细的了解请移步论文:《Noisy Activation Functions》,同时下图给出示例:
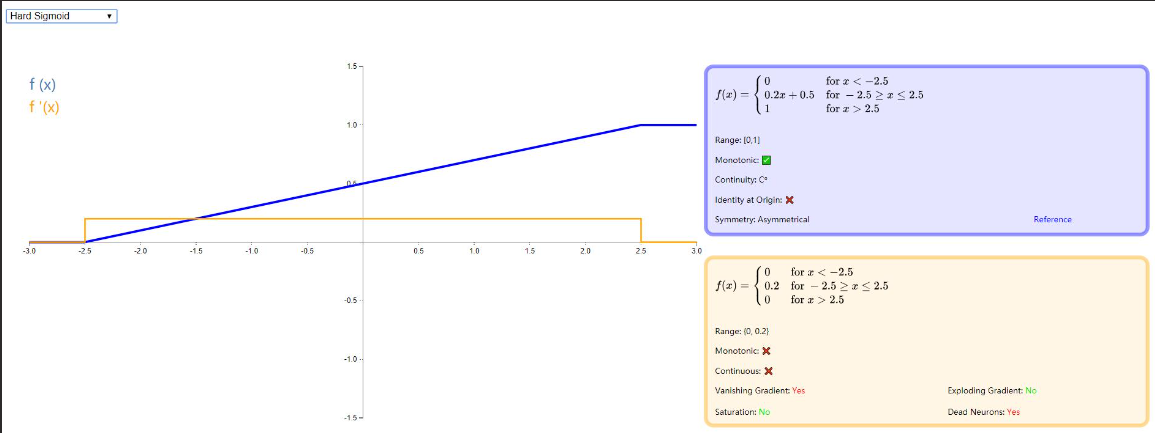
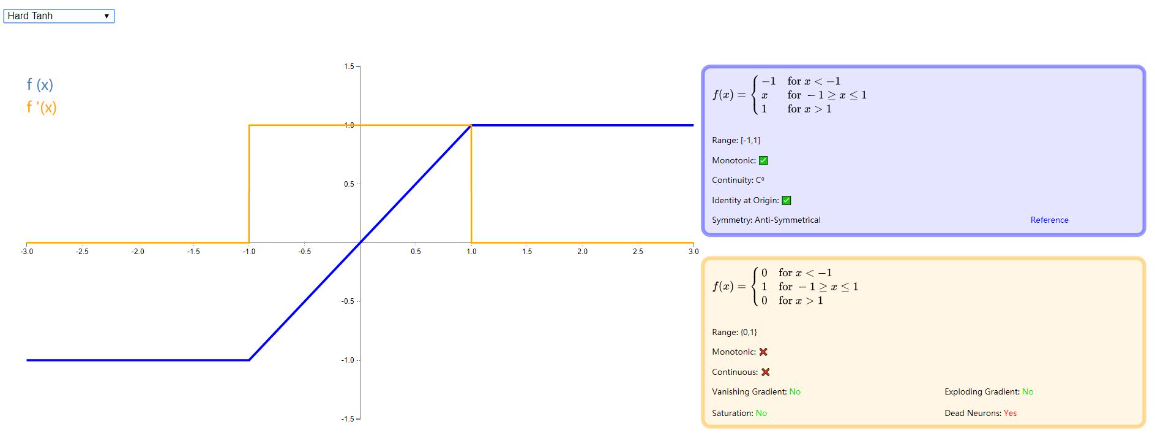
Hard Tanh
Hard Tanh 其实跟 Hard Sigmoid 类似,都是为了加快训练过程而使用线性函数段来近似替代原有的激活函数,同样有 ReLU 不可避免的神经元死亡问题。论文:《Noisy Activation Functions》,跟上一个激活函数出自同一篇论文。
图示如下:
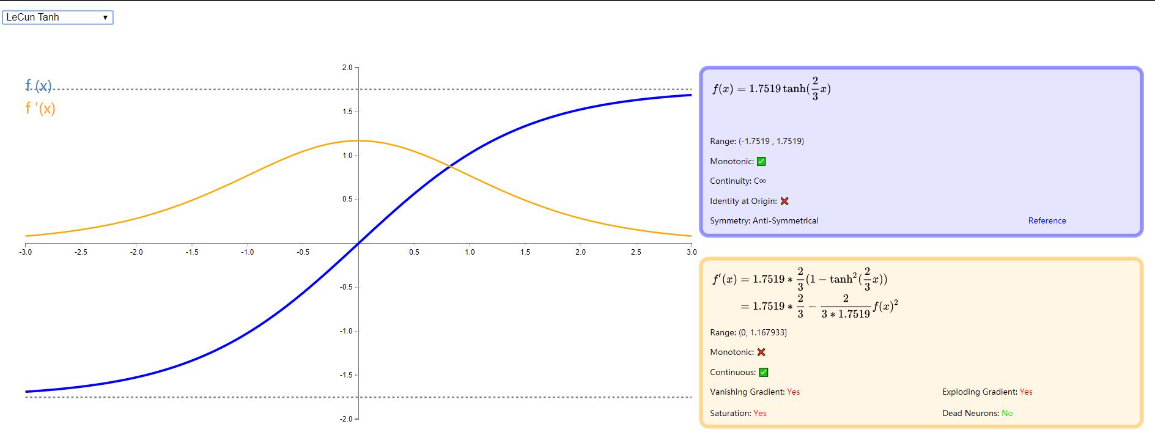
LeCun Tanh
有时也被称作 Scaled Tanh, 它是 Tanh 的一种缩放版本,由 Yann LeCun 在论文《Efficient BackProp》 中提出,它有一些可以提高学习效率的属性:f(±1)=±1;导数最大为 1;有效收益接近 1。更详细的介绍请移步论文,下图给出示例:
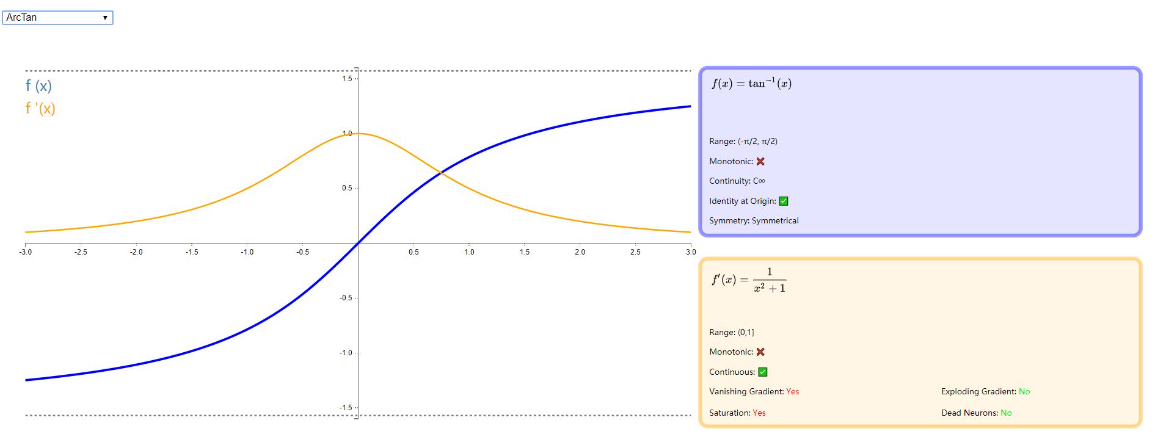
ArcTan
ArcTan 从图像中看着类似于双曲正切(Tanh)函数,ArcTan 相比 Tanh 更平缓,默认情况下,其输出范围为:(−Π,Π)。从其导函数可以看出导数趋于零的速度比较慢,因此训练比较快。
图示如下:
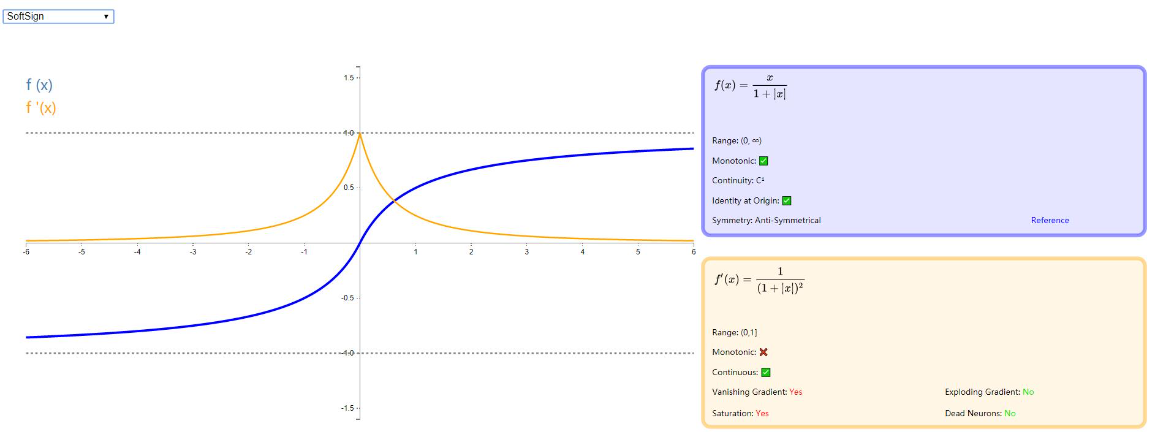
SoftSign
SoftSign 也是一种类 Tanh 的激活函数,以 0 点为中心反对称,取值范围为 (−1,1),除了在 0 点的导数难计算外,训练速度也比较快。详情可以参考论文:《Quadratic Polynomials Learn Better Image Features ∗》,图示如下:
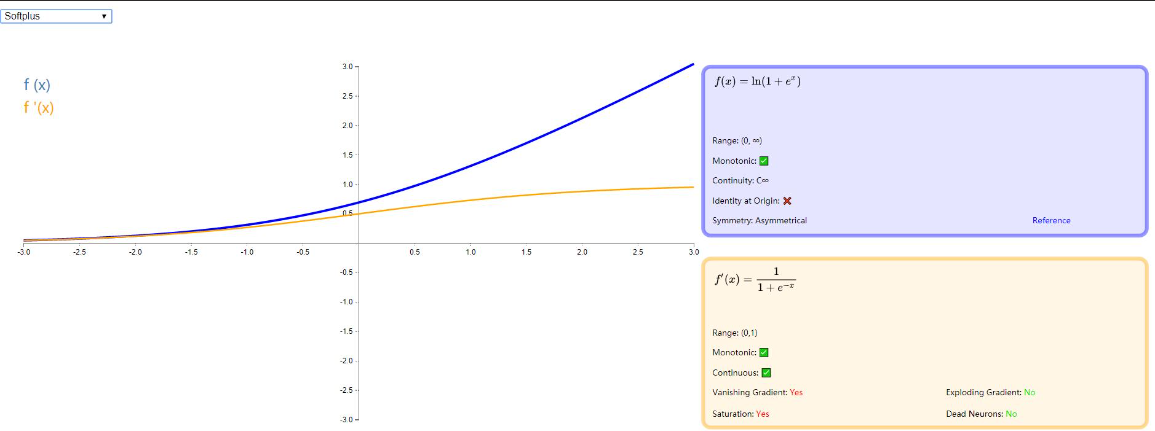
SoftPlus
SoftPlus 作为 ReLU 的平滑替代品,可以返回大于零的任何值。与 ReLU 不同,它的衍生物在任何地方都是连续的和非零的,可以防止死神经元。然而,与 ReLU 不同的是,它不对称且不以零为中心,这可能会妨碍学习。此外,由于导数总是小于 1,消失的梯度可能是一个问题。有兴趣的可以阅读这篇论文:《Deep Sparse Rectifier Neural Networks》
图示如下:
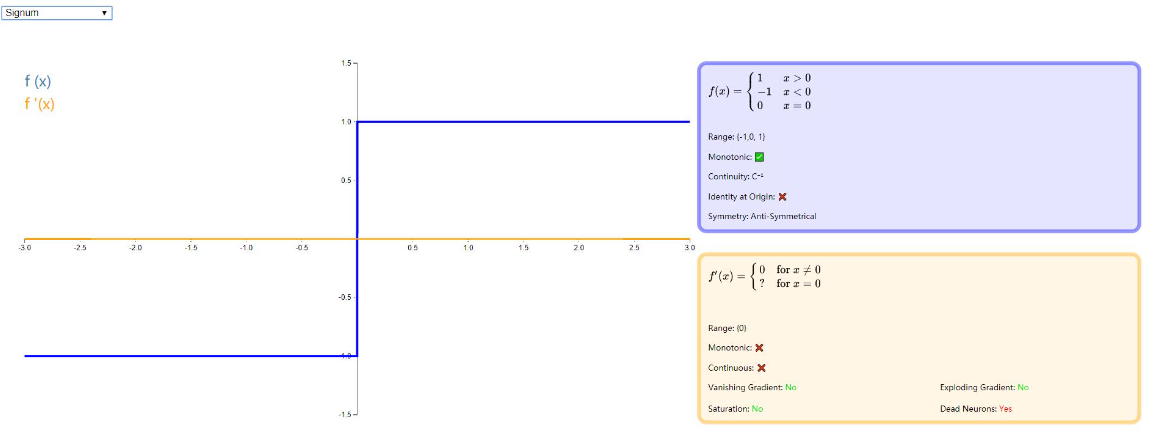
Signum
Signum(或者 Sign)是二进制步激活函数的缩放版本。对于负值和正值,它分别取值 - 1 和 1,在原点处取零。虽然缺乏阶梯函数的生物学动机,但该函数是反对称的,这被认为是激活函数的有利特征。图示如下:
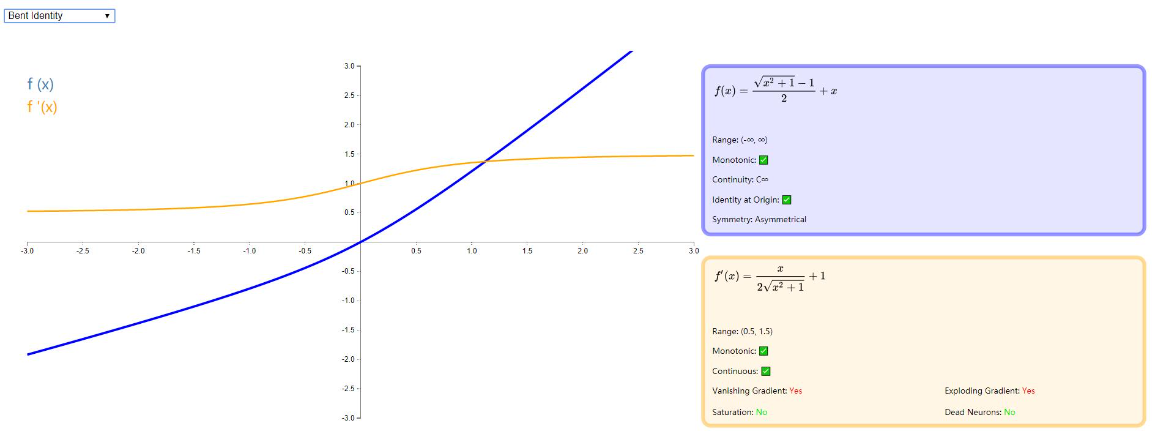
Bent Identity
在 Identity 和 ReLU 之间的一种折中,Bent Identity 允许非线性行为,而其非零衍生物促进有效学习并克服与 ReLU 相关的死神经元的问题。由于它的导数可以返回值 1 的任意一侧,因此它可能容易受到爆炸和消失的梯度的影响。图示如下:
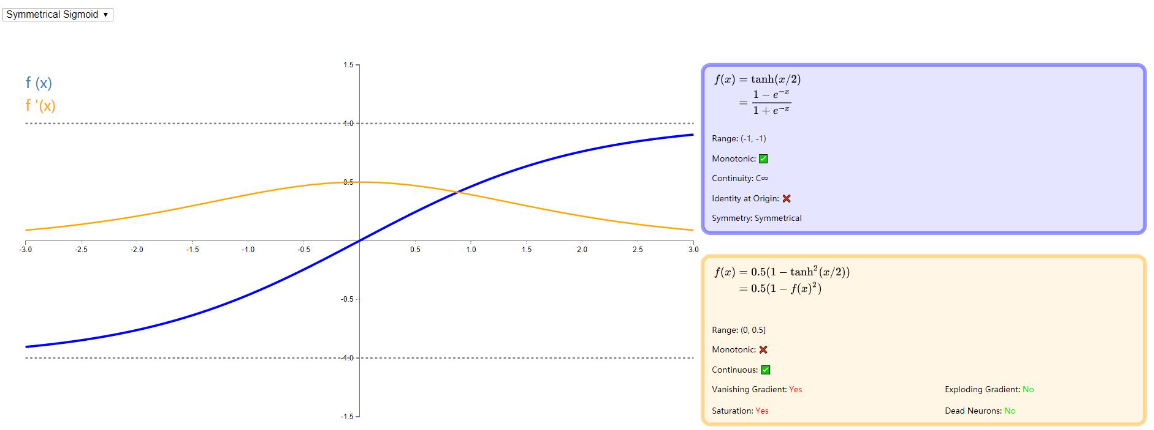
Symmetrical Sigmoid
Symmetrical Sigmoid 是 Tanh 激活函数的另一种替代方法(它实际上相当于 Tanh 激活函数输入减半)。像 Tanh 一样,它是反对称的,零中心,可微分并且返回 - 1 到 1 之间的值。它更扁平的形状和更缓慢下降的导数表明它可以更有效地学习。图示如下:
Log Log
log log 返回 0 到 1 之间的值,log log 激活函数是经典 sigmoid 的潜在替代。它更快地饱和并且在原点处具有超过 0.5 的值。详细可以从下图看出:
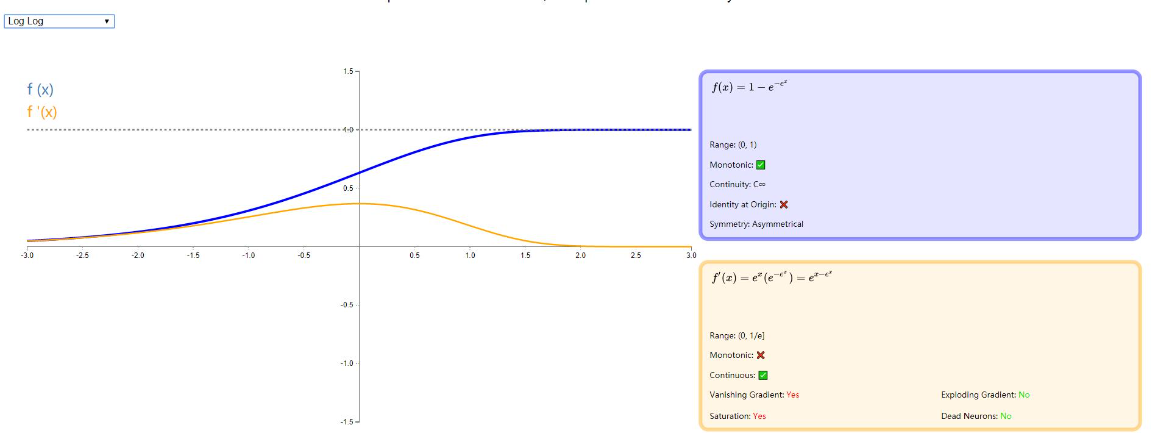
Gaussian
相信大家对高斯函数都比较熟悉了,这种激活函数更具理论性而非实际性,模仿生物神经元的全有或全无特性。它对神经网络没有用,因为它的导数是零(除了 0,它是未定义的)。这意味着基于梯度的优化方法是不可行的。图示如下:
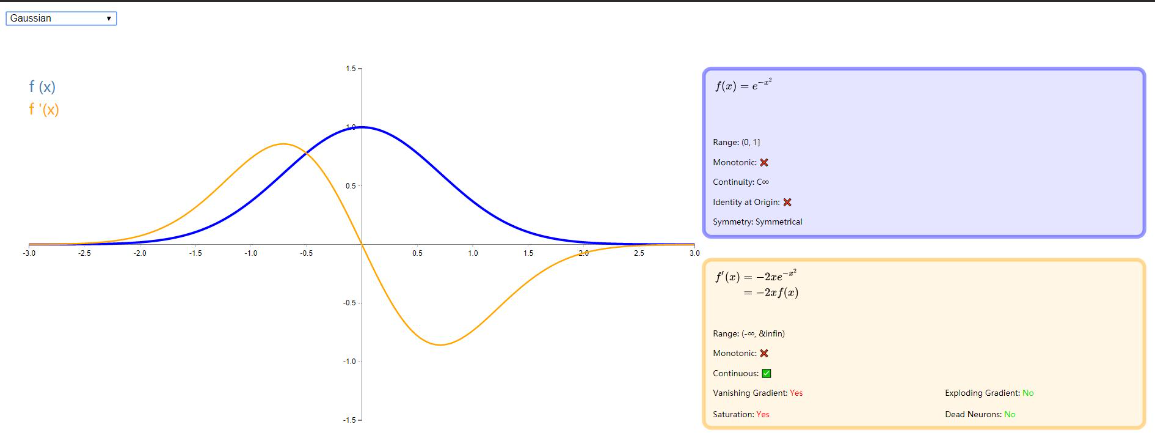
Absolute
顾名思义,Absolute 激活函数返回输入的绝对值。它的导数很容易计算,除了 0 以外的任何地方定义。由于导数的大小等于 1,这种激活功能不会受到消失 / 爆炸梯度的影响。图示如下:
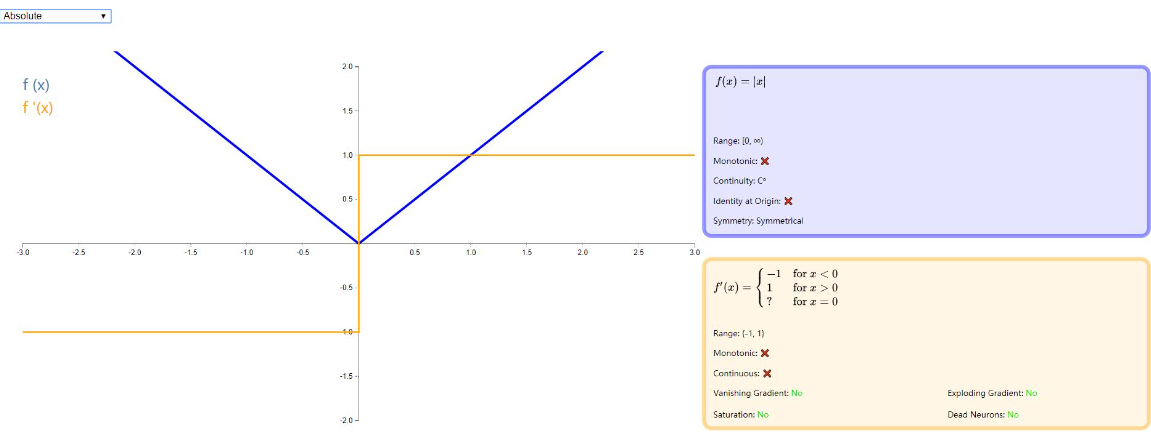
Sinusoid
通常称作 sin (x) , 这个大家都比较常见,毕竟伴随我们学习生涯很久了,就不在做过多解释了,看下图吧:
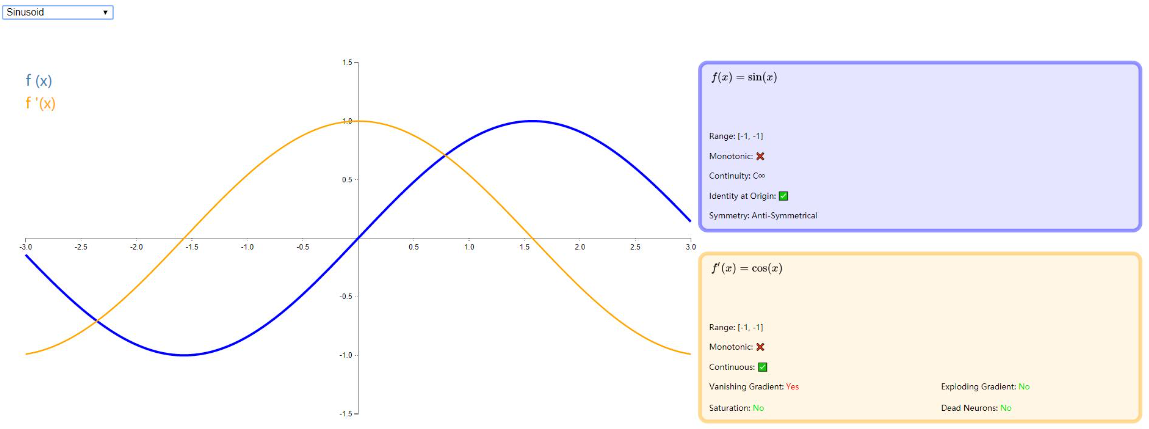
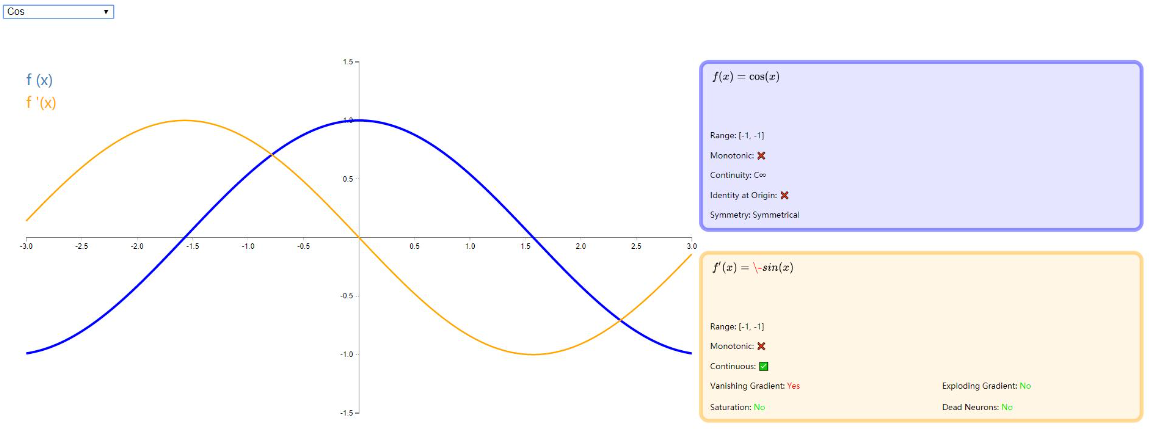
Cos
如图:
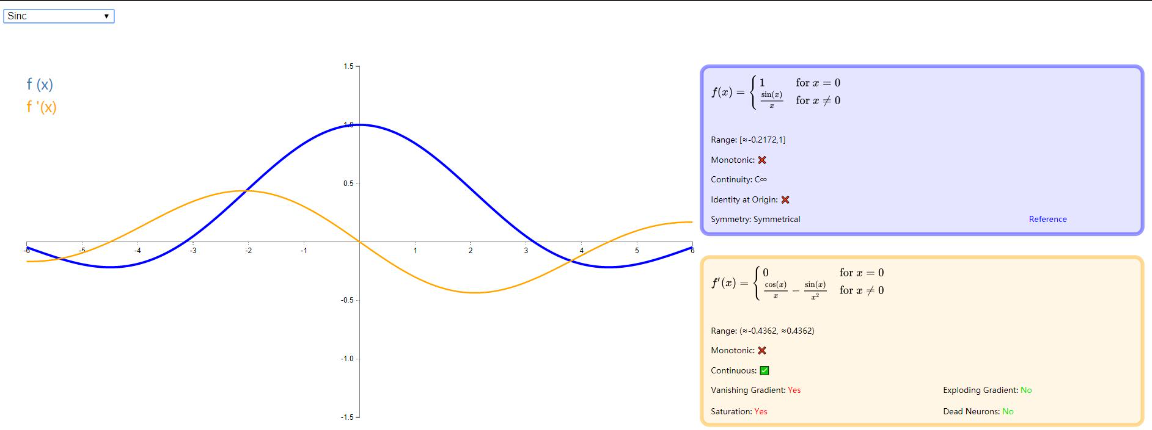
Sinc
如图:
参考文献
http://spytensor.com/index.php/archives/23/#menu_index_1
- 神经网络激励函数的作用是什么?有没有形象的解释? - 颜沁睿的回答 - 知乎
- 《Rectified Linear Units Improve Restricted Boltzmann Machines》
- 神经网络回顾 - Relu 激活函数
- Sigmoid 函数总结
- 《Rectifier Nonlinearities Improve Neural Network Acoustic Models》
- 《Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification》
- 《Empirical Evaluation of Rectified Activations in Convolutional Network》
- 《Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)》
- ELU 激活函数的提出
- 《Self-Normalizing Neural Networks》
- 《Deep Learning with S-shaped Rectified Linear Activation Units》
- 《Noisy Activation Functions》
- 《Efficient BackProp》
- 《Quadratic Polynomials Learn Better Image Features ∗》
- 《Deep Sparse Rectifier Neural Networks》
